
 | |
| Volume 10, Number 3 | March 4, 2020 |
In Part I of this series, the theory that congenital disease is the essence of biological aging was advanced. Part II presents a simple empirical derivation of this theory.
One of the simplest experiments a scientist can perform to study aging is to chart the number of survivors versus time for a group of same-age animals.
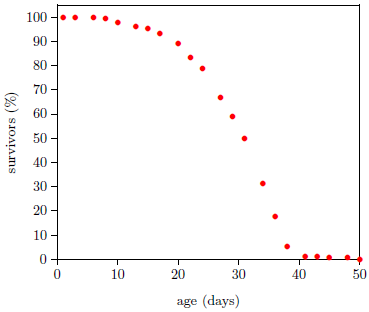 |
Figure 1 shows life span data for fruit flies ( Drosophila melanogaster) raised in my laboratory in 2001. To obtain these data, a cohort of 264 wild type Drosophila, all of the same age, were raised in a single chamber. Three times each week, the fruit flies' food was changed, and the number of dead flies was counted and recorded. Figure 1 shows the percentage of flies still living as a function of age. Day zero corresponds to emergence of the flies from pupation.
A graph of the Figure 1 type is called a survival (or survivorship) curve. Survival curves show the percentage of survivors as a function of age for a population of organisms.
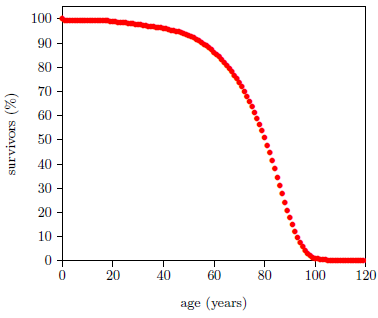 |
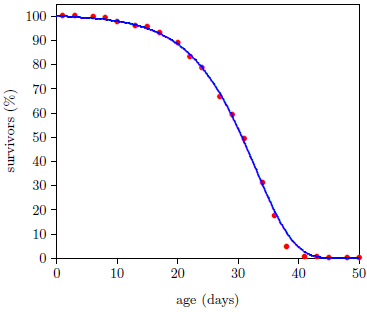
Survival curves can be plotted for all species, including humans. When we plot such a curve for humans today (Figure 2), we find that the shape of the curve is similar to that for fruit flies (Figure 1), even though the time axis is very different in the two cases. This ski-hill shape is, in fact, characteristic of well-cared-for organisms in general. It is definitive of aging. Specifically, the portion of the survival curve displaying increasingly rapid falloff with increasing age is what scientists have in mind when they talk about aging. In popular terms, this shape means that most individuals in the initial group live a "full" life before dying of "old age."
Survival curves are generally reasonably well characterized mathematically by a Gompertz function. This function has the (differential) mathematical form:
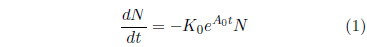
where N is the number of survivors at time t, K0 is a proportionality constant, e signifies the natural exponential function, and A0 is an exponential growth constant.
A few simple observations help give insight into the meaning of this equation. First, the left side of the equation, dN/dt, represents the number of individuals dying per unit time. It is just the death rate at any given time. The minus sign on the right side of the equation shows that the number of survivors decreases with time. Also on the right side of the equation, notice that at any time, t, the death rate is proportional to N, the number of survivors at that time. This is as it should be, of course. If one doubles the number of individuals in the group, then the number of individuals dying per unit time (the death rate) should also double.
The significance of the constant K0 can be clarified as follows. The probability of death in a given time interval is defined as the number of individuals dying during the time interval divided by N, the number of individuals at the start of the interval. The number of individuals dying in the time interval is just N - Nfinal, where Nfinal is the number of individuals surviving at the end of the time interval. By definition of the differential, this is -dN. Thus, the probability of death is -dN/N. In the present case, this probability can be found by simple rearrangement of Equation 1.
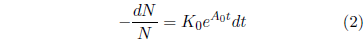
At t=0, this equation reduces to K0 = (-dN/N)/dt. The constant K0 is thus seen to specify the probability of death of an individual per unit time at t=0.
Finally, the eA0t part of the right side of Equation 1 says that the probability of death per unit time increases exponentially with time. This is made explicit by Equation 2. The constant A0 controls how quickly the probability of death per unit time increases.
Equation 1 may be integrated to yield an expression for N as an explicit function of t. The result, for A0 ≠ 0 is:
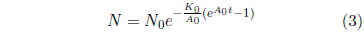
This is the Gompertz function in its integrated form. It can be used to model survival curves resulting from biological aging.
This equation is graphed as a blue line in Figure 3 (using N0=100, K0=0.001 per day, and A0=0.159 per day) and in Figure 4 (using N0=99.219, K0=9.1 ×10-5 per year, and A0=0.0815 per year). The Gompertz function obviously does a good job of characterizing real experimental survival curve data. (It is not expected to do a perfect job in the present case because, among other things, the survival curve data shown contain an admixture of deaths not due to aging, such as deaths due to automobile accidents in the case of U.S. males.)
 |
 |
While all the Gompertz function does, mathematically, is specify an exponentially increasing probability of death from birth on, this, nonetheless, results in a good characterization of real experimental survival curve data. This tells us that biological aging is characterized by an exponentially increasing probability of death from birth on. Now here is the critical question. Why should aging be characterized by an exponentially increasing probability of death from birth on?
To find a rational answer to this question, perform the following thought experiment.
Imagine (leaving ethical questions aside) a cohort of a thousand peacefully coexisting modern young men, raised together since infancy on a desert island, with adequate shelter, but with no natural food supply. Airlift food and drink to them so they have a normal, balanced diet. When they reach age 25, withhold food but not water. Keep this up until the last of the thousand has died.
What will be observed, of course, in the weeks following removal of food from the diet, is an outbreak of the disease we call starvation. Since this disease is ultimately fatal when left untreated, it will eventually claim the lives of the entire cohort.
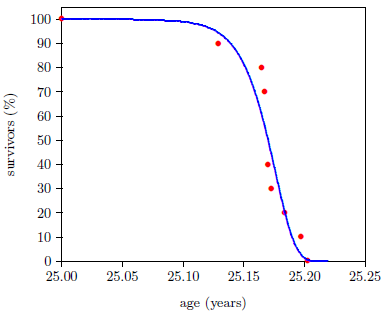
Figure 5 shows what may be expected. It shows survival curve data (red dots) for ten Irish hunger strikers who died of starvation.[1] These ten hunger strikers were all males, ranging in age from 23 to 29. For the present purpose, which calls for a same-age group, the average age of the ten hunger strikers (25 years) has been used.
 |
The advent of starvation causes the mortality rate to begin to climb. Because human bodies are varied genetically, and because each individual's interaction with the environment is unique, the entire cohort does not all die at the same time. Some genetic constitutions will be more resistant to the ravages of starvation than others, and some individuals will experience less stressful interactions with the environment than others. But after a few weeks, individuals will begin to die of this disease. As time goes on, the probability of death will increase, and the longer time goes on, the more quickly the probability of death will increase.
Interestingly—tellingly—survival curve data for starvation can be characterized by a mathematical function very similar to the Gompertz function. The blue line in Figure 5 is a graph of the equation
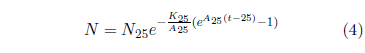
using N25=100, K25=1.330 ×10-3 per year (from the 2013 actuarial table data cited in Figure 2), and A25=61 per year.
Notice that the blue line curve has the characteristic ski-hill shape. It looks very similar to the Gompertz curve describing aging. The only major difference is that it begins at age 25 years instead of at birth. In fact, Equation 4 reduces exactly to the Gompertz function of Equation 3 if 25 is everywhere replaced by 0 in Equation 4.
Like the Gompertz function, the kernel of Equation 4 is an exponentially increasing probability of death with time. This is shown more clearly by its differential form:
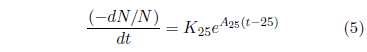
In Equation 4, the 25 is clearly specific to the case of the hunger strikers in question. In the general case, starvation can be initiated at any arbitrary age. Let T represent the age of onset of the disease. Then Equation 4 can be generalized as follows:
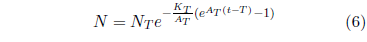
Starvation is just one example of a class of diseases characterized by Equation 6. It describes any disease having an exponentially increasing probability of death when left untreated. This is a large class of diseases. All nutritional deficiency diseases—for example, dehydration or scurvy or pellagra—belong to it. The class is not inclusive of all diseases, of course. Most infectious diseases—for example, chicken pox or the common cold—obviously do not belong to it.
Because T, the age of onset of the disease, may, in principle, be adjusted to any value, it may be adjusted to T = 0. When this is done, Equation 6 becomes the Gompertz function equation describing biological aging. Thus, the Gompertz function is seen to be merely a special case of Equation 6. Evidently, biological aging is indistinguishable from any exponentially progressing, ultimately fatal, universally present (i.e., present in all members of the population) disease which happens to be active starting at birth.
It might be felt that this is true only if one restricts to mathematics and survival curve shapes—that clinical symptoms could be used, for example, to differentiate between congenital disease and biological aging. How? What clinical symptom is there which is uniquely and universally definitive of biological aging? The clinical symptoms of biological aging in fruit flies are significantly different from the clinical symptoms of biological aging in humans.
Biological aging is not defined by any set of clinical symptoms. In real life, it cannot be defined this way. Rather, it is defined "as an age-dependent or age-progressive decline in intrinsic physiological function, leading to an increase in age-specific mortality rate…"[2]—i.e., as a ski-slope survival curve starting from birth.
Any exponentially progressing, ultimately fatal, universally present congenital disease will give rise to "an age-dependent or age-progressive decline in intrinsic physiological function, leading to an increase in age-specific mortality rate." Thus, any such disease active in real life will simply be seen as and be called "biological aging."
Every indication, both theoretical / mathematical and experimental / clinical is that biological aging is indistinguishable from any exponentially progressing, ultimately fatal, universally present congenital disease. The simplest explanation of why this should be the case is that biological aging is, in fact, nothing more than exponentially progressing, ultimately fatal, universally present, congenital disease. This immediately yields the theory that the essence of biological aging is congenital disease. ◇
The Biblical Chronologist is written and edited by Gerald E. Aardsma, a Ph.D. scientist (nuclear physics) with special background in radioisotopic dating methods such as radiocarbon. The Biblical Chronologist has a threefold purpose: to encourage, enrich, and strengthen the faith of conservative Christians through instruction in Biblical chronology and its many implications, to foster informed, up-to-date, scholarly research in this vital field within the conservative Christian community, and to communicate current developments and discoveries stemming from Biblical chronology in an easily understood manner. The Biblical Chronologist (ISSN 1081-762X) is published by: Aardsma Research & Publishing Copyright © 2020 by Aardsma Research & Publishing.
|