
 | |
| Volume 10, Number 7 | April 24, 2020 |
Several issues back I wrote:[1]
In Addendum to Aging: Cause and Cure, three long-lived mice were of special interest.[2] The oldest of these three mice was still living when the addendum was published. She died about two months later. I am eager to report on the implications of this mouse's unusually long life span, but I need to lay some groundwork before doing so. To begin with, I need to introduce a general theory of aging to provide a scientific framework within which to understand and discuss the phenomenon of aging in a generalized way. I expect to follow this with a quantitative analysis of how the anti-aging vitamins are likely to alter human life expectancies. Once this groundwork has been laid, we should be ready to have a look at the significance of the final long-lived mouse's unusual longevity.
 |
I have finished laying the groundwork mentioned above, but I find that there is yet more groundwork needing to be laid. The General Theory of Aging developed in BC102,[3] BC103,[4] and BC105[5] sheds new light on survival curves, and this affects how they should be analyzed. Before entering into a discussion of the implications of the long-lived mouse's life span, the method that will be used to analyze her group's survival curve data needs to be explained. Consequently, this issue is devoted to technical background material which many lay readers may want to skip over. There is no harm in doing so. A look at some important implications of pre-Flood human life spans is planned for the next issue, and a discussion of the long-lived mouse is planned for the following issue.
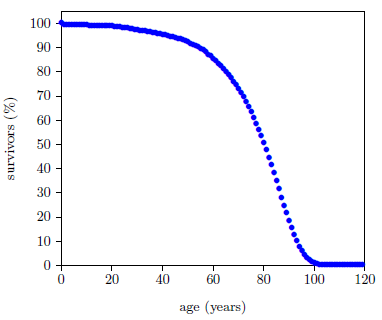
Figure 1 shows survival curve data for U.S. males. These data are for the year 2016 from the United States Social Security Administration's actuarial tables.[6] They will be used in the following pages to illustrate the least-squares data analysis method which the General Theory of Aging prompts.
Traditionally, the Gompertz function has been used as a model for survival curve data. The General Theory of Aging reveals that this function is not entirely right for the job.
The Figure 1 survival curve is clearly dominated by aging. That is, most of the deaths are due to aging. That is why the number of survivors falls off so rapidly after about age 60—aging is killing nearly everybody off.
While aging is the dominant cause of death, it is not the sole cause of death. The data of Figure 1 contain an admixture of deaths not due to aging. For example, there is a noticeable infant mortality in the very first year of the graph. Less conspicuous, but equally real, are deaths due to traffic accidents. In fact, there are deaths due to hundreds of causes other than aging in this dataset: everything from homicides to lightning strikes.
Let us call deaths which are not due to aging, "extraneous" deaths. The Figure 1 graph is made up, then, of two components: (1) deaths due to the aging disease and (2) extraneous deaths.
The Gompertz function is, in general, not well suited to describing extraneous deaths. We have previously seen that the Gompertz function describes an exponentially increasing probability of death per unit time with calendar age.[7] There is no reason why the probability per unit time of being struck by lightning should increase exponentially with the calendar age of the individual being struck. Does a 40-year-old have a much greater chance of being struck by lightning than a 20-year-old, and does a 60-year-old have a yet much greater chance of being struck by lightning than a 40-year-old?
The Gompertz function is an approximation only. It smears together many independent causes of death, most of which are not expected to be exponentially increasing with age. The Gompertz function gets away with this wherever the survival curve is dominated by deaths due to aging because the aging disease is characterized by an exponentially increasing probability of death per unit time, as we have previously seen.[8]
Mathematically, at least two terms are required to describe what is really going on with real-life survival curve data. One term is needed to describe deaths due to aging, and another term is needed to describe extraneous deaths.
It might be thought that what is needed, then, is (1) a Gompertz function to describe deaths due to aging, and (2) some other function to describe extraneous deaths. But, as it turns out, the Gompertz function doesn't describe aging deaths quite properly either. The Gompertz function happens to be a workable approximation for aging deaths, but it is not quite right.
The General Theory of Aging clarifies that aging is exponentially progressing congenital disease. In developing the General Theory of Aging, two-cycle engines were used to illustrate possible "congenital diseases" leading to "death" of the machines.[9] Lack of lubricating oil leading to wear of piston rings and consequent loss of compression was given as one example. Ablation of the spark plug electrode was given as a second example. And clogging of the air filter was given as a third example.
Taking these three cases as representative of general aging diseases, notice that they all require some passage of time before the first death appears. For piston rings to wear sufficiently for the machine to become inoperable, the machine must be operated for some amount of time. For the spark plug electrode to wear away by ablation, some finite number of sparks must be generated, and this means that the machine must be operated for some amount of time. For the air filter to become clogged, air must be pulled through it, and this means that the machine must be run for some amount of time.
For these three examples, there will be no deaths due to these aging diseases when the machines are new. Said more precisely, the rate of death of these machines due to each of these three aging diseases when the machines are brand new is zero.
This seems to be a general property of aging diseases. It seems intuitive that the initial probability of death due to aging must be zero since initially (i.e., at t=0) there has not yet been any aging.
Curiously, the Gompertz function, which otherwise describes aging so well, does not allow the initial rate of death to be zero.
The Gompertz function has the differential form:
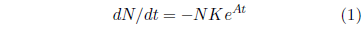
In this equation, t is the time (generally specified as the age of the organism for survival curves), N is the number of individuals surviving at time t, dN/dt is the population growth rate (the negative sign in the equation says that the population is shrinking [due to deaths]), K is the probability of death per unit time at t = 0, and eAt specifies an exponential increase in the probability of death per unit time, the rapidity of which is controlled by A.
At t = 0, Equation 1 reduces to:
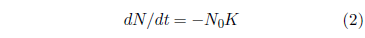
This is the initial rate of death, and it is not zero. N0, the initial number of machines, is not zero, of course. K is also not zero. Equation 1 shows that if K were zero, then the rate of death would always be zero for all time. This means that there would be no death and no aging and all machines would go on living forever. For aging to be present, K cannot be zero. Thus, neither N0 nor K is zero, and this means that the Gompertz function excludes the very real case of the initial rate of death being zero for an aging disease.
Thus, surprisingly, the Gompertz function is found to describe properly neither death due to aging nor extraneous deaths.
Why, then, does the Gompertz function do a good job of describing real-world, aging-dominated survival curves? It is because it smears together aging deaths and extraneous deaths, and extraneous deaths can reasonably have a non-zero rate of death at t=0. There is, for example, no need for any passage of time for a lightning strike to cause a death. A lightning strike can kill a brand new machine the instant it comes off of the assembly line.
When aging deaths and extraneous deaths are separated out, the Gompertz function is no longer useful. We very much desire to separate aging deaths from extraneous deaths because we wish to study aging specifically, not deaths in general. When studying aging specifically, extraneous deaths act as a background interference, obscuring what we are trying to learn about. It is, therefore, necessary to part company with the Gompertz function at this point.
Having bid a nostalgic farewell to the Gompertz function, we now find ourselves in need of a function which properly describes aging deaths. As it turns out, a suitable function can be obtained by a modification of the Gompertz function. The right side of Equation 1 can be made to be zero at t=0 as follows:
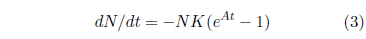
This equation is no longer the Gompertz function. It is distinctly different from Equation 1, which defines the Gompertz function. A retains its meaning, as the exponential growth constant, but the meaning of K is changed. It is no longer the probability of death per unit time at t=0. For Equation 3, the probability of death per unit time at t=0 is, by design, zero. K is now simply a proportionality constant, acting as a "gain" control for the exponential increase from zero of the probability of death per unit time.
While Equation 3 is no longer the Gompertz function, it retains everything the Gompertz function does correctly in regard to aging and adds in the benefit of having a zero rate of death at t=0. It will be utilized in place of Equation 1 to describe aging deaths from now on.
To describe real-life survival curve data accurately, we need also a function which describes extraneous deaths. The rate of extraneous deaths is obviously complicated. For humans, it will be different in a time of war than during peacetime, for example. Extraneous deaths can have many different causes and, consequently, many different functional forms.
A general approach in such a case might be to use a Taylor series to approximate the function describing the rate of extraneous deaths. This gives:
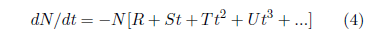
I have found that dropping all but the first term in this series works well in practice for lab data. One expects this to work well in practice because, for controlled laboratory survival curve data, one chooses experimental conditions deliberately to minimize extraneous deaths, and the strong (i.e., exponential) time dependence of death due to aging is expected to kill off the population before higher order, t-dependent terms in Equation 4 can grow large enough to have much impact on the death rate.
This gives as an approximation for the rate of extraneous deaths:
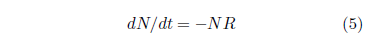
In this equation, R specifies a constant probability of death per unit time due to extraneous deaths. This approximation finds considerable support from its long-standing use within the Gompertz–Makeham law of mortality, where it supplies the Makeham term.
The equation describing real-life survival curve data in this approximation, combining both deaths due to aging and random (i.e., having a constant probability of occurrence, independent of time) extraneous deaths, is then:
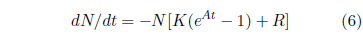
In this equation, as K increases, the death rate due to aging increases, and as R increases, the death rate due to random extraneous deaths increases. The solution of this differential equation is:
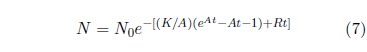
This is the model which I will use in all that follows, including, eventually, analysis of the survival curve data for the long-lived mouse's group. I will call it the "Aardsma model" to be clear that we are no longer using the Gompertz function.
Notice that this model takes into account only one cause of aging. Additional terms are needed in the model if two or more congenital aging diseases are present having nearly equal dominance. In practice, one expects only a single congenital disease to show up at a time in most cases because the exponential increase in death rate due to the most dominant aging disease is likely to have killed off the population before the next most dominant congenital disease has begun to have much of an effect on the death rate.
Notice also that, in this approximation, the total rate of deaths separates into a time dependent component (due to aging deaths) and a time independent component (due to constant background "noise" deaths).[10] The constant background "noise" deaths are due to random events like lightning strikes. Thus, the model's applicability is limited to survival curves where extraneous deaths are due to random events. Rather than calling these "random extraneous deaths," I will use the shorter "random deaths" to mean the same thing from now on.
Survival curve data points do not all have the same measurement uncertainty. As a result, it is necessary to weight the data points to obtain the optimum fit of the model.
In any survival curve experiment, the fundamental observation is the number of deaths in a time interval. For the actuarial life table data of Figure 1, the data points are for 1 year time intervals, each interval corresponding to a given age. The number of deaths which occurred in each age interval can be obtained from the actuarial table. For example, the 2016 actuarial table shows that, for a total of 100,000 males dying in 2016, 230 died in their 41st year (i.e., between their 40th and 41st birthdays), and 462 died in their 51st year.
These numbers of deaths are not to be taken as exact. Imagine breaking the total number of U.S. males who died in 2016 (roughly 1,400,000) into randomly chosen groups of 100,000. The number of deaths in the 41st year age interval would not be exactly 230 for every one of these groups. Basic counting statistics teaches that the number of events counted from group to group will fluctuate as the square root of the average for that age interval. This means that the 230 of the 41st year is to be treated as 230 ± 15.2 deaths, and the 462 of the 51st year as 462 ± 21.5 deaths.
This illustrates that the number of deaths corresponding to each age interval have varying measurement uncertainties. When carrying out a least-squares fit of a given model to measured data, it is intuitive that data points having less uncertainty should be given relatively more weight in determining the optimum values of the model's parameters (i.e., A, K, and R in Equation 7 for the Aardsma model). A weighted least-squares analysis is, therefore, required. This is accomplished in the usual way, by assigning each data point a weight equal to the square of the reciprocal of its uncertainty.
Error bars depicting the size of the uncertainties associated with each data point are normally displayed graphically with the data. In the present case of the 2016 actuarial data, the error bars are too short to be visually discerned on the graph. The error bar for the 51st year, for example, plots as a vertical line through the data point at x=50.5 years and y=91.747 percent survivors. It has a total length of (2×21.5/100,000×100=) 0.0430%—much too short to be seen on the graph.
For usual lab experiments, the number of experimental animals used is much smaller than the number of males included in the 2016 actuarial life table, and this results in much larger error bars which are generally easily discerned graphically.
It is necessary to use a computer to carry out the mathematical computations needed to perform the least-squares fit. Algorithms for this task have been around for a long time and do not need to be coded from scratch. I have used functions (FCHISQ, FUNCTN, and FDERIV) and subroutines (CURFIT and MATINV) written by Bevington in Fortran IV and published in 1969.[11] Both FUNCTN and FDERIV were adapted by me, as intended by Bevington, to suit the present model.
When a weighted least-squares fit of the Aardsma model to the 2016 actuarial life table data for males is carried out, the fitted curve shown in Figure 2 results. (I have excluded the first data point from this fit because the large infant mortality it reflects is not included in any way in our simple model.) The fit is visibly good (not great), but the goodness of fit parameter, reduced chi-square (Χ2ν), has a value of 1316, which says the fit is statistically extremely poor. For a good fit, Χ2ν is expected to be near 1.
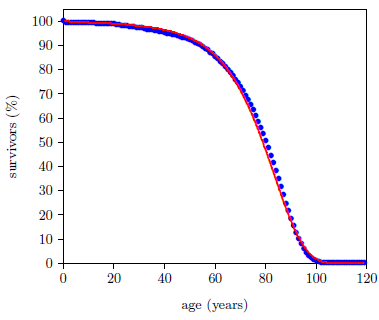 |
The large value of Χ2ν in this instance is not characteristic of normal laboratory survival curve data. It happens because the fit, in this instance, is extremely poor. Visually, it looks not all that bad, but relative to the (microscopic) error bars on the data points, it is terrible. For such tiny error bars, the fitted curve resulting from a good fit would be seen to pass through the approximate center of each blue data point on the graph. Our fitted curve does not do this. It is visibly off center much of the time.
The reason our fitted curve doesn't pass through the centers of the data points is because our simple model does not adequately describe all that is going on with this survival curve. Our simple model adequately describes the deaths due to aging in this data set, and it adequately describes random deaths in this data set. These two terms explain a great deal of what is going on with this data set, but they do not explain everything. Because our model does not describe infant mortality, I excluded the first data point from the fit, as mentioned above. To include infant mortality in the model, another term would need to be added to the differential rate of death equation (Equation 6). But, as there is a lot more than just infant mortality going on with the extraneous deaths in this data set, many more terms are needed for a complete description. For example, notice that beginning around age 20, the data points begin to fall noticeably below the fitted curve. By roughly age 35, the data points (represented by blue dots having diameters much larger than their error bars in all cases) and the fitted curve are barely even touching one another. This says that there is a systematic loss of young men from this survival curve which has nothing to do either with aging or with random deaths. And indeed, according to the Center for Disease Control and Prevention (CDC), for the year 2016, 13.4% of deaths in the 20–44 years age range were due to suicides, 9.6% were due to homicides, and another 1.0% were due to HIV disease.[12] Our simple model includes none of these extraneous deaths.
Here again this 2016 actuarial survival curve for U.S. males is seen to be different from controlled laboratory experimental survival curves. The sorts of extraneous deaths it involves do not generally present themselves in lab experiments. Neither mice nor fruit flies use guns lethally or commit suicide, for example. But this survival curve does a very good job of teaching some of the finer points of modeling survival curve data sets via least-squares, which is why I have chosen to use it in this article.
The goodness of fit, Χ2ν, can be improved by increasing the uncertainties in the individual data points. This is a deliberate workaround, having no other purpose than to approximate more accurately the uncertainties in the fitted model parameters A, K, and R. In effect, this workaround shifts the blame for the poor fit over to the uncertainties in the data points, saying that they are unrealistically too small. In reality, of course, it is the model which has the problem—it has too few terms to describe what is really going on with the data set. By expanding the data points' error bars, all by a constant factor, we bring the data into closer harmony with the model by making the fine structure in the data, due to extraneous deaths, become small relative to the (inflated) uncertainty in the data points.[13]
This workaround does not affect the values of the fitted parameters in any way. Only their estimated uncertainties are affected. Multiplying all error bars by a constant factor does not change the relative weights of the various data points, so the final fit is the same. Again, the reason for expanding the error bars to get a better goodness of fit value is purely to obtain more realistic estimates of the uncertainties in the final parameters from the available dataset. Expanding the error bars on the data points by a constant factor increases the estimated uncertainties in the fitted parameters by the expansion factor.
In practice, this workaround is implemented automatically by the computer program in all cases. The factor by which the uncertainties of all the data points need to be multiplied to obtain Χ2ν = 1 is just the square root of Χ2ν. Thus, the computer program merely multiplies the estimated uncertainties in the parameters by the square root of Χ2ν at the conclusion of the least-squares analysis. For the 2016 actuarial male survival curve, this workaround increases the estimated uncertainties in the fitted parameters by a factor of 36. For laboratory survival curve data, this workaround generally results in a much more modest (10 or 20 percent) adjustment of the estimated uncertainties of the parameters.
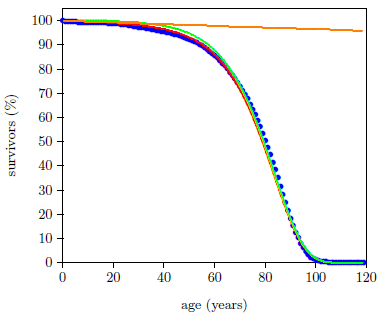
Because the Aardsma model cleanly separates deaths due to the aging disease from random deaths, it allows these two contributions to the survival curve data set to be studied in isolation from each other. The least-squares estimated survival curve due to aging alone results from setting R to zero in Equation 7 while otherwise using the values for A and K found by the least-squares fit. Similarly, by using the value for R found by the least-squares fit in Equation 7 while setting K to zero, the least-squares estimated survival curve due to random deaths alone results. These two cases are shown in Figure 3. ◇
 |
The Biblical Chronologist is written and edited by Gerald E. Aardsma, a Ph.D. scientist (nuclear physics) with special background in radioisotopic dating methods such as radiocarbon. The Biblical Chronologist has a fourfold purpose: to encourage, enrich, and strengthen the faith of conservative Christians through instruction in biblical chronology and its many implications, to foster informed, up-to-date, scholarly research in this vital field, to communicate current developments and discoveries stemming from biblical chronology in an easily understood manner, and to advance the growth of knowledge via a proper integration of ancient biblical and modern scientific data and ideas. The Biblical Chronologist (ISSN 1081-762X) is published by: Aardsma Research & Publishing Copyright © 2020 by Aardsma Research & Publishing.
|
^ Gerald E. Aardsma, "A General Theory of Aging: Part I," The Biblical Chronologist 10.2 (February 12, 2020): 1. www.BiblicalChronologist.org.
^ Gerald E. Aardsma, Addendum to Aging: Cause and Cure (Loda, IL: Aardsma Research and Publishing, July 26, 2019), page 8. www.BiblicalChronologist.org.
^ Gerald E. Aardsma, "A General Theory of Aging: Part I," The Biblical Chronologist 10.2 (February 12, 2020): 1–4. www.BiblicalChronologist.org.
^ Gerald E. Aardsma, "A General Theory of Aging: Part II," The Biblical Chronologist 10.3 (March 4, 2020): 1–4. www.BiblicalChronologist.org.
^ Gerald E. Aardsma, "A General Theory of Aging: Part III," The Biblical Chronologist 10.5 (March 31, 2020): 1–5. www.BiblicalChronologist.org.
^ ssa.gov/oact/STATS/table4c6.html (accessed March 2, 2020).]
^ Gerald E. Aardsma, "A General Theory of Aging: Part II," The Biblical Chronologist 10.3 (March 4, 2020): page 2. www.BiblicalChronologist.org.
^ Gerald E. Aardsma, "A General Theory of Aging: Part II," The Biblical Chronologist 10.3 (March 4, 2020): pages 3–4. www.BiblicalChronologist.org.
^ Gerald E. Aardsma, "A General Theory of Aging: Part III," The Biblical Chronologist 10.5 (March 31, 2020): pages 1–2. www.BiblicalChronologist.org.
^ That Equation 3, describing aging, contains only time dependent terms can be seen by carrying out a Taylor series expansion of the exponential around t=0, followed by the subtraction.
^ Philip R. Bevington, Data Reduction and Error Analysis for the Physical Sciences (New York: McGraw-Hill Book Company, 1969).
^ www.cdc.gov/healthequity/lcod/men/2016/all-races-origins/index.htm (accessed 2020/04/10).
^ My son, Matthew, on reviewing a draft of this article for me, summed up this workaround this way: "Basically what is happening is that if you want to use this simple model to approximate a complex population, you are going to 'pay' for it by increased uncertainties in the modeled parameters."