
 | |
| Volume 4, Number 2 | March/April 1998 |
In the Volume 3 Number 5 issue of The Biblical Chronologist I proposed that the root physical cause of Noah's Flood was a collision between a very high speed cosmic projectile (i.e., a "space rock") and Earth.[1] Since then several subscribers have sent me newspaper clippings or similar items reporting on recent theoretical investigations by scientists of the effects of asteroid impacts on Earth. These clippings report that scientists find catastrophic phenomena of several sorts associated with such impacts: global fires, tidal waves, dust from the impact blocking out the sun for long periods of time with consequent global cooling, mass extinctions of life, and so forth.
These popular reports are helpful in coming to grips with the facts that: 1. cosmic projectiles of various sorts do exist, 2. they can occasionally collide with the earth, and 3. they can have devastating consequences for life when they do so. But when it comes to the Flood these reports can be somewhat misleading. The reason for this is that even a very large asteroid impact is a tiny thing relative to the collision with the cosmic projectile which caused Noah's Flood, as I show quantitatively below.
But if asteroid impacts can produce global catastrophes and mass extinctions of life, and they are tiny compared to the Flood impact, then how could any life have survived the Flood impact—even with the building of an ark? This is the central conundrum for the Flood impact hypothesis. Can this hurdle be cleared, or must we seek some other root physical cause of Noah's Flood?
A descending fireball, brighter than the sun, exploded over a sparsely populated area in the Tunguska region of Siberia on June 30, 1908.[2] Over 300,000 acres of pine forest were leveled in an instant. The explosion was heard over 600 miles away. The trees were later found to be snapped off and pointing radially away from the center of the blast (Figure 1), except at the center of the impact, were no trace of the original forest remained.
 |
The Tunguska event is believed to have been caused by the explosion of a 50 to 60 meter diameter object (i.e., an object large enough to fill half a football field) in the atmosphere some 8 kilometers above the ground.[3] Whether this object was an icy fragment of a comet or a rocky asteroid is unclear. The energy of the blast is estimated today at between 10 and 20 megatons—the equivalent of a hydrogen bomb.
The energy for the explosion was furnished by the Tunguska object's mass and very high speed. The average speed of a meteoroid entering Earth's atmosphere is about 20 kilometers per second (over forty thousand miles per hour) and this is the probable speed of the Tunguska object. Explosion of the object resulted from the braking action of the atmosphere. Very large aerodynamic forces act on an object in the atmosphere at such high velocities. These tend to break the object down into smaller pieces. These smaller pieces offer an even larger surface area for atmospheric braking. The result is further, even more rapid fragmentation and heating. This process rapidly snowballs, culminating in the catastrophic disintegration of the object and release of its enormous kinetic energy in a short distance—i.e., the object explodes.
For objects only a few tens of meters in diameter, the explosion generally takes place in the atmosphere. Larger objects are able to penetrate to the ground where they explode due to collision with the surface material of the earth. Such collisions produce craters, of which Meteor Crater in Arizona is probably the best-known example.
The Tunguska object is an example of a large class of objects which might collectively be called "space debris". This class includes comets (having an icy composition), asteroids (rocky or metallic), and the fragments of comets and asteroids called meteoroids. (Meteorites are meteoroids which have fallen to the surface of the earth.)
The asteroids provide what is probably the best analog of the cosmic projectile which caused the Flood. Asteroids are big chunks of rock or metal which are found, like the planets, to be a part of our solar system. Unlike the planets, however, which are few in number, the asteroids are very numerous.[4]
Today, more than 6000 asteroids have been observed well enough for their orbits to be determined accurately, and tens of thousands more have been observed only briefly.And while the planets are massive bodies, the asteroids are relatively small. Ceres, for example, the largest known asteroid, is less than one quarter the diameter of the Moon.
The asteroids range in size from almost 1000 km in diameter, down to small rocks or dust particles. Gehrels has estimated that there are about half a million asteroids larger than 1.6 km in diameter. Since the vast majority of asteroids are so small, however, the total mass of the asteroid belt is also quite small. If all of the asteroids were lumped together, their total mass would probably be less than one-thousandth the mass of the Earth.[5]
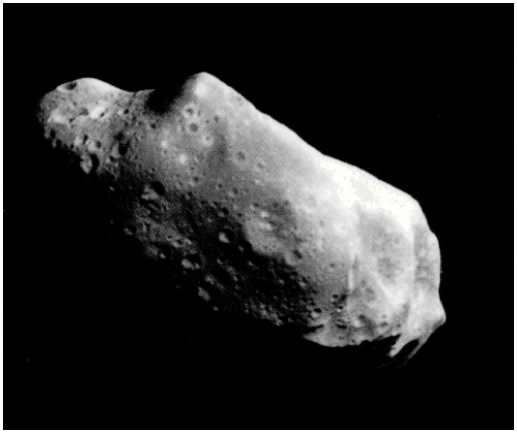
Figure 2 shows a NASA image of asteroid 243 Ida acquired by the Galileo spacecraft in 1993. This chunk of rock is 55 kilometers long, 24 kilometers wide, and 20 kilometers thick.
 |
Asteroids orbit the sun like the planets do. Most are found in the so-called "asteroid belt" between the orbits of Mars and Jupiter. Other orbits are possible however, including ones which intersect Earth's orbit about the sun. In such cases a collision results if both the asteroid and the Earth arrive at the intersection point at the same time. And even asteroids whose orbits do not intersect Earth's orbit pose some threat of collision because asteroids can be perturbed into new orbits by collisions with one another and by close encounters with massive bodies such as Jupiter.
A great deal of research has gone into the question of how great a threat is posed to civilization today by asteroid collisions with Earth. A Tunguska-like event over a large city could obviously result in very many lives lost. Events of this size are not the biggest concern, however. Because asteroids come in sizes much greater than the Tunguska object, there is some potential for much larger disasters than even the destruction of a large city. In fact, for collisions with asteroids having diameters greater than about one kilometer, scientists talk in terms of global disaster.[6]
Fortunately, the probabilities of collisions with such large objects are relatively small. Tunguska-like events are believed to happen only once every 250 years on average, and the probability of a global-scale event is estimated at about one per 500,000 years.[7] Nonetheless, international research into possible means of detecting Earth-threatening asteroids early enough to allow for their deflection or destruction has been under way for a number of years now.[8]
While the asteroids seem to provide adequate analogs to the Flood projectile in terms of possible size and probable material composition, it seems most unlikely at the present time that the Flood projectile came from the asteroid belt. It appears, in fact, that the Flood projectile was foreign to Earth's neighborhood—that it entered the solar system from the vast reaches of space beyond. Its energy was enormous relative to even very large asteroid impacts, which suggests that its incoming velocity was far too large for it to have been a member of the solar system.
Every indication is that the Flood projectile represents a category of cosmic collision far beyond that which is represented by the asteroids and comets. Its energy was sufficient not only to produce devastating global effects, but, indeed, to melt the globe! The question which begs answering is how any life could possibly have survived the collision of the Flood projectile with Earth—ark or no ark. Why did a mere hemispherical Flood result, instead of the oceans being entirely vaporized, and the crust of the earth besides?
I have sought an answer to this apparent conundrum over the past several weeks, and I am happy to report that I have found one. My purpose in this article is first of all to make this conundrum quantitatively explicit, and then to show what I believe to be its resolution. In the process of doing these things a thorough conception of what took place in the opening minutes of the Flood should emerge.
To achieve this purpose an excursion into the field of physics is unavoidable. For readers who are unfamiliar with the basic physics concepts and mathematical tools needed in the present study, I have used a format which allows one to easily skip over the physics and math and still follow the basic discussion and conclusions. An introductory Question explains the problem. The physics and math necessary to find the answer to the question follow in a separate Physics section. Then the answer itself is summarized and discussed in an Answer section.
What was the energy of the Flood projectile?
The energy of a cosmic projectile determines how big the explosion will be when it collides with Earth. It is the sudden release of this energy which produces the explosion, and it is this energy which drives subsequent effects such as the lofting of dust into the atmosphere to block out the sun, or the production of tidal waves. Thus, to understand the scale of the collision in question it is of first importance to determine the energy of the Flood projectile.
To obtain this energy we must work from what we know about the phenomena of the Flood, inventorying the energy used in each instance. Recall that in the hemispherical Flood model (in which we are presently working) the inner core of the earth is displaced until it collides with the mantle.[9] This displacement is caused by the solid earth acquiring a new velocity due to the impact of the cosmic projectile. And one consequence is the heaping of the water of the southern oceans up in the northern hemisphere together with the water of the northern oceans. Such phenomena require a great deal of energy to accomplish. This energy must all be supplied by the incoming projectile.
As it turns out, the velocity given to the earth by the projectile yields the dominant energy item in this inventory. The resulting kinetic energy of the earth is greater than 2.4×1029 joules. This compares, for example, with 1.8×1025 joules to lift the southern oceans onto the top of the northern oceans, and about 5×1024 joules to source one inch of rain per hour globally for forty days and nights.
The kinetic energy given to the earth by the cosmic projectile was calculated as follows. The equation for the kinetic energy is:
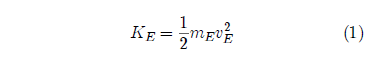
where mE is the mass of the earth and vE its velocity due to collision with the Flood projectile. (Strictly speaking one should use the mass of the earth minus the mass of the inner core in this equation, but the subtraction of the mass of the inner core has no effect on the result at the precision to which we are presently working.) I obtained the minimum value for vE from the motion of the inner core relative to the crust and mantle after the impact as follows.
First, I calculated (numerically) the energy required to move the inner core of the earth from its normal central position out to the mantle using the equation:
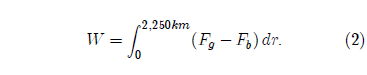
Fg is the force due to gravity, and Fb is the force of buoyancy experienced by the inner core. I used the density figures for the inner and outer core and whatever other parameters were needed from the Preliminary Reference Earth Model in this calculation.[10] I found 7.4×1028 joules.
This work energy must come from the initial kinetic energy of the inner core after impact (viewed from a stationary Earth reference frame) plus the kinetic energy of the circulating outer core fluid. Recall that we have previously seen that the outer core fluid must have been set in a circulating motion by the impact since this motion is necessary to explain the fact that the inner core was held pinned to the mantle for many days.[11]
The motion of the fluid outer core and its interaction with the inner core are not well characterized at this point. However, it is clear that the outer core could have no greater kinetic energy per unit mass than the inner core. To do so would mean that the outer core fluid was circulating more rapidly than the fastest motion of the inner core. This is not possible because the inner core is what "stirred" the outer core fluid into motion in the first place.
Thus it is possible to set the maximum kinetic energy of the outer core for a given velocity of the inner core to:
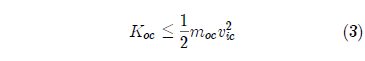
where Koc is the kinetic energy of the outer core, moc is the mass of the outer core, and vic is the initial velocity of the inner core after impact.
Meanwhile, the initial kinetic energy of the inner core is just:
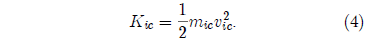
Thus the initial kinetic energy of the entire core must be:
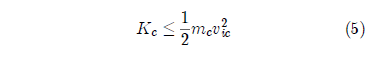
where mc = mic + moc = 1.9×1024 kg.
As mentioned above, the energy required to lift the inner core to the mantle must come from this initial kinetic energy. Thus:
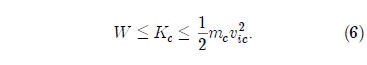
Therefore:
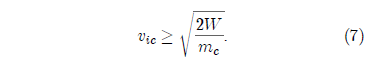
Substitution of values at this stage gives vic ≥ 2.8×102 m/s as the initial velocity of the inner core after impact in the stationary Earth frame.
If we now switch into the moving Earth, stationary inner core reference frame we see immediately that vic = -vE, where vE is the velocity given to the crust and mantle of the earth by the Flood projectile. Thus we find that the crust and mantle of the earth were given a velocity greater than 2.8×102 m/s by the impact.
Substituting this value for vE, and 6.0×1024 kg for the mass of the earth, mE, into equation 1 yields 2.4×1029 joules as the minimum kinetic energy given to the earth by the collision with the Flood projectile, as stated above.
This is not a good estimate of the minimum kinetic energy of the Flood projectile itself, however. It seriously underestimates that quantity. The reason for this is that it is physically impossible to channel 100% of the kinetic energy of the projectile before impact into kinetic energy of the earth after impact. In fact, only a very small fraction of the kinetic energy of the incoming projectile can be converted into kinetic energy of the earth.
The collision of the Flood projectile with the earth is a completely inelastic collision. Because of momentum conservation we must have:
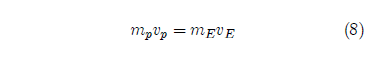
where mp and vp are the mass and velocity of the incoming projectile, and mE and vE are the mass and velocity of the earth as previously defined. We can use this equation to obtain an equation for the ratio of the kinetic energy given to the earth by the Flood projectile to the kinetic energy of the Flood projectile itself.
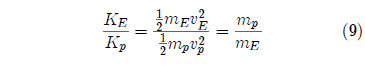
This shows that the fraction of incoming kinetic energy given to the earth will be equal to the ratio of the mass of the projectile to the mass of the earth.
Several things indicate that this ratio will be very small—that the mass of the Flood projectile must have been quite small relative to the mass of the earth. First, if the projectile were comparable in size to the earth, then one would need to imagine a high speed collision between two roughly equal size objects. The consequence would surely be catastrophic fragmentation of both objects—and this does not harmonize at all with Noah's observations.
Second, the space rocks which we know about (i.e., the asteroids) all have diameters less than 1000 kilometers, as noted above, and the vast majority have diameters much less even than this. This is much smaller than the earth's 12,000 kilometer diameter.
Third, we have so far found that the Kara Sea seems the most probable impact center for the Flood projectile.[12] It has a diameter of only about 420 kilometers. Thus, even if the Flood projectile filled it completely (which seems unlikely), its diameter would still be only about one thirtieth that of the earth. This implies a mass ratio (for equal density objects) of 1:28,000.
Thus it seems inevitable that the ratio of the mass of the projectile to the mass of Earth must be 10-3 or smaller.
When substituted into the previous equation this says that, at best, only one part in a thousand of the incoming projectile's kinetic energy was converted to kinetic energy of the earth.
Thus we are led to fix the minimum energy of the Flood projectile at 2×1032 joules, with a more probable value at least ten times this amount.
This is an enormous energy. Scientists consider 2×105 megatons (MT) to be the nominal threshold for global disaster.[13] The minimum energy of the Flood projectile we have just found is 5×1016 MT! This is 250 billion (2.5×1011) global disasters all rolled up in one!
Clearly, there was more than enough energy to pile the oceans of the world up in a great water mountain over the north impact pole, and to drive an ocean-high tsunami, as previously found.[14] There was also plenty of energy to move the inner core of the earth to the mantle[15] and plenty of energy available to evaporate forty days and nights worth of heavy rainfall.
The difficulty, however, is that there appears to be entirely too much energy for any life to survive through the Flood, as mentioned above. The problem is that even when we add up all the energy required to do all of the things we know happened at the time of the Flood—moving the inner core to the mantle, lifting the southern oceans onto the northern ones, etc.—we still have almost all of the projectile's original energy left over. It is a fundamental law of science that energy cannot be destroyed. Where did all this energy go?
Normally, extraneous energy ends up as heat, and we would expect it to do so in this case. But we encounter an enormous problem if we convert all of this leftover energy to heat, as the answer to the next question shows.
Suppose the excess energy of the incoming projectile was used to heat up the earth. How hot would the earth become?
To get a feel for this, approximate the heat capacity of the entire earth with that of steel at 25°C, i.e., c = 447 J/kg/K. Then a quantity of heat, ΔQ, will produce a temperature change in the entire earth of:
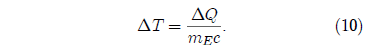
Substitution of values from above into this equation yields ΔT = 7×104 K.
This is well above the boiling point of all of the elements. A more elaborate calculation incorporating latent heats of fusion and vaporization leads to this same conclusion.
It is found that if the excess energy of the incoming projectile were used to heat up the earth, the entire earth would be vaporized! This obviously disagrees with both Noah's observations of the Flood and with our present experience.
Before I begin to tackle the question of how to solve this conundrum, there is another problem which I need to make explicit.
We are imagining that the Flood projectile collided with the earth and was brought rapidly to rest as a result. We are further imagining that the earth acquired its new velocity as an immediate result of this collision. This presents a considerable difficulty to objects loosely connected to the surface of the earth, such as the ark and its occupants.
I showed above that the minimum velocity given to the earth in the collision was 280 meters per second. This is 630 miles per hour.
What would happen if the earth beneath your feet suddenly acquired a velocity of 630 miles per hour?
The result would be similar to the well-known stunt of pulling the tablecloth out from under the china; if you pull the cloth out very quickly the china will all stay in its place. The problem for Noah and the ark, however, is that the surface of the earth, unlike tablecloths, has mountains in it. This means that the ark and all its occupants would be crashed into, at 630 miles per hour, by the first mountain that came their way.
Noah's failure to record such an episode might easily be explained—there is, after all, almost no chance of surviving such a high speed crash. But Noah's evident ability to record subsequent events is then rendered somewhat enigmatic.
Thus, two serious problems appear if one attempts to assign the root cause of the Flood entirely to a simple collision between the Flood projectile and Earth: too much energy is unleashed upon the earth, and the transfer of momentum from the projectile to the earth is too sudden. It is obviously necessary to go beyond this simple collision model if we are to satisfy the constraints of the Biblical narrative.
There is really only one way to solve the excess energy problem. This energy must not be allowed to remain with the earth. It must be sent back out into space where it came from.
There is also only one way to solve the sudden transfer of momentum problem. The earth's new momentum must not be acquired all at once. It must be acquired more slowly, over a relatively protracted period of time. Notice that if the acceleration of the tablecloth is slow enough, the china will move together with the tablecloth—a much more acceptable outcome in the case of the ark.
I can think of only one way of satisfying both of these requirements. We must go beyond the simple collision model and incorporate a "rocket engine" into our thinking about the Flood.
Notice that any rocket faces problems parallel to the two we have found for the simple collision model. The space shuttle, for example, contains a great deal of energy in its chemical fuel at launch time. I have done no calculations on this but I suspect it contains enough energy to vaporize the entire shuttle, just as the Flood projectile contained enough energy to vaporize the earth. But the shuttle is not vaporized by the release of this energy because the energy is all shot away from the shuttle by its rocket engines. Also, the space shuttle achieves very high velocities, just as the earth did at the time of the Flood. But the astronauts do not all suddenly crash into the walls of the shuttle at takeoff because the rocket engines spread the acceleration out over a protracted period of time. The shuttle acquires its large velocity slowly, rather than all at once.
The secret to the solution to both of these problems in the case of the shuttle is seen to reside with the rocket engines. They automatically solve both problems. This suggests that we must somehow equip the earth with a "rocket engine" at the start of the Flood to solve the problems of the simple collision model. How can this be done? I suggest the following model.
We imagine the cosmic projectile, rather than exploding at the surface of the earth, puncturing a deep vertical shaft into the earth, and exploding at the bottom of the shaft. This is just an extension of what we know happens at lower energies. Lower energy asteroids lose their energy high in the atmosphere. Larger asteroids puncture a channel some distance into the atmosphere before exploding. Still more energetic asteroids puncture a channel completely through the atmosphere and explode at the surface of the earth. (This punctured channel is called a "wake" in the technical literature. Adushkin and Nemchinov define the wake as "a rarefied channel through which some part of the [impact] energy can escape the dense layers of the atmosphere".[16]) It is obviously reasonable to suppose that the more energetic an asteroid is, the deeper it will penetrate into the earth before exploding. The extreme energy of the Flood projectile suggests the possibility of penetration to considerable depth before explosion.
The explosion vaporizes a portion of the earth at the base of the shaft, producing a chamber of highly pressurized, very hot gas. This gas is kept "bottled up" by the surrounding earth. The only way the chamber can vent is through expulsion of gas back up the shaft.
This is a rudimentary rocket engine. The explosion chamber parallels the combustion chamber of a rocket engine, and the shaft is like the exhaust nozzle.
Because of the extreme temperature and pressure within the explosion chamber the gas is expelled at extremely high velocity from the shaft. This produces a thrust on the earth which begins to give it a new velocity, just as the expulsion of air from a toy balloon propels the balloon about the room, or as the expulsion of hot gas from a rocket engine produces a thrust which propels the rocket.
The thrust continues until the chamber gases are exhausted, most of the enormous energy of the projectile having been shot back out into space in the form of hot gas.
Because of the small mass of the Flood projectile relative to the mass of the earth, very little momentum is given to the earth by the collision itself. Instead, the earth's new velocity develops gradually as a result of the protracted thrust of the rocket engine which the collision of the Flood projectile has both created and ignited.
This, I suggest, is what actually happened at the time of the Flood.
Does this all work out when investigated quantitatively? The following set of questions and answers shows that, in fact, it does.
What minimum speed must the atoms of the hot ejected gas have for this rocket solution to work?
The hot gas must escape Earth's gravity. Otherwise the gas will just be pulled back to Earth. This will result in no net thrust, and in the Flood projectile's energy being returned to Earth.
Thus the hot gas must be ejected with a speed greater than or equal to the escape velocity for Earth. This velocity is vesc = 1.12×104 m/s (i.e., 25,000 miles per hour).
What temperature does this correspond to?
The most probable speed for atoms in a gas is related to the temperature through the expression
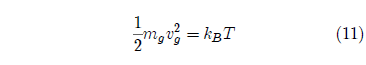
where mg and vg are the mass and the velocity of the gas atoms, kB is the Boltzmann constant, and T is the absolute temperature of the gas. Choose oxygen as the atom involved since it has the highest terrestrial abundance. Then mg = 16×10-3/6.0×1023 kg, vg = vesc = 1.1×104 m/s, and kB = 1.38×10-23 J/K. These values yield T = 1.2×105 K.
Thus the ejected gas must have a temperature in excess of one hundred thousand degrees. This is very high, but it is still a thousand times lower than the temperature achieved in a helium thermonuclear reaction.[17]
Can this "Flood rocket" provide enough thrust to achieve the necessary new velocity of the earth?
The minimum momentum given to the earth is mEvE = (6×1024 kg)(3×102 m/s) = 2×1027 kg m/s. This momentum now comes from the mass, me, and velocity, ve, of the hot ejected gas. Thus meve ≥ 2×1027 kg m/s. Setting ve = vesc I find me = 2×1023 kg.
Thus, the Flood rocket can provide adequate thrust as long as 2×1023 kilograms of gas are ejected at Earth's escape velocity. This corresponds to about 3% of Earth's mass being vaporized and ejected. Less mass is needed if the gas is ejected at higher velocity. Since enough mass is available to provide the needed thrust even at the lowest possible velocity, there is no problem achieving the necessary momentum of the earth in the Flood rocket model.
What is the minimum kinetic energy of the Flood projectile in the Flood rocket model?
The kinetic energy taken away by the ejected mass is
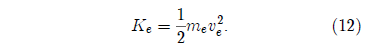
Using the value of meve found in the previous question, this becomes Ke ≥ 1×1027ve J. Substituting ve = vesc once again yields Ke ≥ 1×1031 J.
The minimum Flood projectile energy is now found to be 2×1015 MT. This is about twenty times less than the minimum energy found previously for the simple collision model.
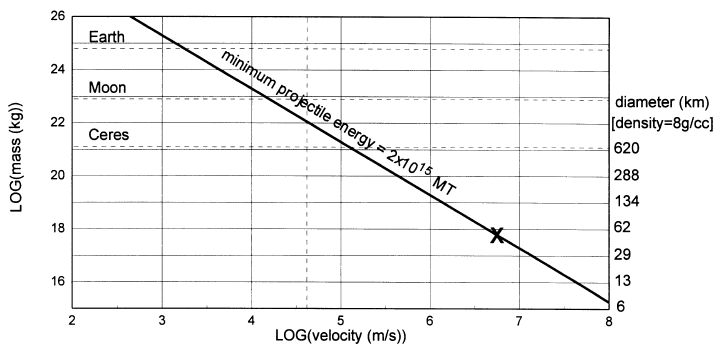
Figure 3 shows a graph of projectile mass versus projectile velocity. (Notice that this is a logarithmic graph—each grid line goes up by a factor of 10 over the previous grid line.) The minimum energy of the Flood projectile which was just found is plotted as the heavy solid line on this graph. The masses of Earth, Moon, and Ceres (the largest known asteroid), are indicated by horizontal dashed lines. The vertical dashed line shows the highest speed an object can have at Earth and still remain bound to the solar system. Thus the asteroids must all have masses less than (below) Ceres, and velocities less than (to the left of) the vertical dashed line. Notice that the minimum projectile energy line does not intersect this asteroid region. This implies that the Flood projectile was probably not a member of the solar system prior to the Flood impact, as stated above. Rather, it seems likely that it entered the solar system from inter-stellar space just prior to its collision with Earth.
 |
What was the Flood projectile made of?
Since the Flood projectile was probably not a member of the solar system, it is impossible to answer this question with anything even approaching certainty. However, there is one asteroid type which seems intrinsically well suited to the job of puncturing a deep shaft into the earth. This is the metallic, iron-nickel, type. Iron-nickel meteorites are found to have densities in the range 7.2–7.9 g/cm3,[18] compared to about 3 g/cm3 for the crust of the earth. They also have a very high mechanical strength.
This group, resembling stainless steel in many ways, has very high density and virtually no porosity (except for nodules) thereby possessing the strongest mechanical structure… Fortunately, the relative abundance of this strong material is thought to be low.[19]
It seems appropriate, as a working hypothesis, to assume an iron-nickel composition for the Flood projectile until any evidence contrary to this assumption may be found.
What was the size of the Flood projectile?
The diameter of a spherical object having a density of 8 g/cm3 is shown by the scale on the right side of Figure 3. It is clear that a wide range of masses is possible for the minimum energy shown.
If the Kara Sea is the impact site, as has been suggested previously and found to be workable so far, then its diameter sets an upper limit of 420 kilometers on the projectile diameter. In actual practice, however, projectile diameters are generally much smaller than the diameters of the craters they make. Thus it seems probable that the Flood projectile was much smaller than 420 kilometers. Perhaps a diameter of 50 kilometers would be an appropriate guesstimate at this early stage of investigation. This is probably not out by more than a factor of ten either way.
For a 50 kilometer projectile the corresponding velocity is 6×10^6 meters per second, as shown by the X in the graph (Figure 3).
What velocity would an object of this mass and velocity impart to the earth upon collision?
The mass of the projectile in this case is 6×1017 kg. This is very much less than the mass of the earth. Thus the velocity given to the earth is
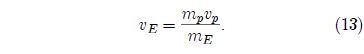
This yields vE = (6×1017) × (6×10^6) / (6×1024) = 0.6 m/s.
The result is 0.6 meters per second, which is just 1.3 miles per hour. Clearly, the collision itself would not produce very much of a jolt for Noah and the ark, which is in harmony with the fact that Noah did not record any jolt at the start of the Flood.
How long would the Flood rocket need to be active to keep the acceleration of the earth acceptably low?
Kane and Sternheim state that a normal takeoff in an aircraft involves an acceleration of about g/2 for 10–20 seconds.[20] (Here g is the acceleration due to gravity at the surface of the earth.) This seems a reasonable permissible upper limit of acceleration for Noah and the ark.
A hot gas ejection time (at ≥ vesc) of 40 seconds is all that is required to keep the acceleration of the ark (at its impact latitude) below g/2. An ejection time of just three minutes reduces the acceleration below what is typically experienced on a fast service elevator, and the Flood rocket would only have to remain in operation for about thirty minutes to render the acceleration of the earth probably undetectable in the ark. All of these ejection times seem within the realm of possibility at this early stage of investigation.
Thus the conundrums faced by the simple collision model appear to be solved by the Flood rocket model. While many more questions could, and ultimately must, be asked of this model, those which have been explored above seem sufficient to demonstrate that the suggestion that the Flood was caused by a collision of a very high speed cosmic projectile with Earth is a reasonable one which must be taken seriously.
This leads to an additional conclusion. The investigation which we have just completed marks the final step in a backwards progression through the Flood. I have previously investigated Noah's observations of the waning of the Flood and found them to be naturally explicable within the hemispherical Flood model.[21] Last issue I reported on an investigation of the waxing of the Flood, which also found ready physical explanations in harmony with Noah's observations.[22] The investigation has now been taken successfully back to the very beginning of the Flood—the moment the cosmic projectile collided with Earth. Thus it seems appropriate to further conclude that the hemispherical Flood model provides a workable explanation of the Flood from start to finish.
To the best of my knowledge the hemispherical Flood model is the only model of the Flood for which this claim can be made. This is true despite the fact that other Flood models have had research man hours invested in them far in excess of the time I have been able to devote to this model.
This seems very significant. It seems most improbable that an event as obviously complex as the Flood should be able to find two differing but equally satisfactory explanations. Because of the enormity of the Flood in so many ways one would expect all false models to rapidly founder on either the Biblical data, or the scientific data, or both. One would expect to be able to find only one explanation of the Flood which was in harmony with both the Biblical record and the principles of science—that single explanation which corresponds to what actually happened at the time of the Flood. The evident success of the hemispherical Flood model relative to all other models strongly recommends it as that single explanation. ◇
It is well known that native peoples from many locations around the globe retain legends of the Flood. Do these legends have anything to teach us about the Flood? How accurate is their "memory" of the Flood?
I have benefitted in regard to these questions from two recent communications from family members which I want to pass along here. These suggest the answer to both of the questions above may very well be, "More than you might at first suppose".
Several issues ago I described what it must have felt like at the start of the Flood as the inner core of the earth began to move toward the north. I wrote:[23]
If the inner core were displaced toward the North Pole it would seem to an observer on the surface of the earth that the direction of horizontal had changed. Surfaces which were previously level would now seem to be tilting downhill toward the North Pole, even though they had not actually moved at all—the local gravitational field is all that would have changed. Water which had been standing on horizontal surfaces before the inner core had been displaced would flow "down" those surfaces toward the North Pole after the displacement. If you were standing on a beach which ran east and west during such a displacement you would see the water of the ocean suddenly begin to flow "up" the beach toward the North Pole. More accurately, you would feel that the ocean had tipped up and that the beach had tipped down so that the water of the ocean was suddenly being poured out across the beach.As the inner core moved toward the north at the start of the Flood, your sum total of experience would cause you to believe that the whole earth around you was inexorably tilting down to the north. Trees growing perpendicular to a previously horizontal surface would remain perpendicular to that surface as you watched the surface slowly tilting downhill to the north. The surface would no longer be horizontal and the trees would no longer be vertical. And all of this would cause you to feel that the whole surface of the ground had tilted, even though the ground had not moved at all—all that had really happened was that the direction of gravity had changed.
The start of the Flood must have been a weird experience, and a memorable one for those who survived the Flood.
Soon after I had explained all of this to my wife, Helen, (my most devoted and cherished supporter) she happened upon a remarkable account in a book she was reading called Childhood and Society. This book is a compilation of the experiences of anthropologists who worked among native peoples earlier in this century. Its purpose, you will understand, is a study of parental practices and attitudes toward childhood in various societies, not a study of Noah's Flood. So the following quote, which appears in the book quite incidentally, came as a considerable surprise to both of us. Fanny is an old Indian woman who functions as a "doctor" to her people, the Yurok Indians of the Pacific coast.[24]
Fanny was in an acute state of gloom when we arrived. Some days before, on stepping out into her vegetable garden and glancing over the scene, a hundred feet below, where the Klamath enters the Pacific, she had seen a small whale enter the river, play about a little, and disappear again. This shocked her deeply. Had not the creator decreed that only salmon, sturgeon, and similar fish should cross the fresh-water barrier? This breakdown of a barrier could only mean that the world disk was slowly losing its horizontal position, that salt water was entering the river, and that a flood was approaching comparable to the one which once before had destroyed mankind.
I found Fanny's "memory" of what the start of the Flood was like, after 5,500 years, just a bit breathtaking! While the idea of "the world disk… slowly losing its horizontal position" is technically incorrect, it is phenomenologically highly accurate.
On top of this, my brother, Allen, who has spent the last year in China with his family, teaching at an A.C.E. school for children of American businessmen stationed there, happened upon the following quote from the school's curriculum:
One legend of the Flood, a Greenland legend, says the earth was flooded because the earth tilted over!
My immediate reaction, once again, was, "Incredible!"
I prefer my brother's reaction though. To fully appreciate it you need to know that, unlike me, he is naturally inclined more toward outdoor adventure than office academics. He wrote, "Wow! If that don't light your fire, your wood's wet!" ◇
The Biblical Chronologist is a bimonthly subscription newsletter about Biblical chronology. It is written and edited by Gerald E. Aardsma, a Ph.D. scientist (nuclear physics) with special background in radioisotopic dating methods such as radiocarbon. The Biblical Chronologist has a threefold purpose: to encourage, enrich, and strengthen the faith of conservative Christians through instruction in Biblical chronology, to foster informed, up-to-date, scholarly research in this vital field within the conservative Christian community, and to communicate current developments and discoveries in Biblical chronology in an easily understood manner. An introductory packet containing three sample issues and a subscription order form is available for $9.95 US regardless of destination address. Send check or money order in US funds and request the "Intro Pack." The Biblical Chronologist (ISSN 1081-762X) is published six times a year by Aardsma Research & Publishing, 412 N Mulberry, Loda, IL 60948-9651. Copyright © 1998 by Aardsma Research & Publishing. Photocopying or reproduction strictly prohibited without written permission from the publisher.
|
^ Gerald E. Aardsma, "The Cause of Noah's Flood," The Biblical Chronologist 3.5 (September/October 1997): 1–14.
^ Charles T. Kowal, Asteroids: Their Nature and Utilization, 2nd edition (New York: John Wiley & Sons, 1996), 39.
^ Vitaly V. Adushkin and Ivan V. Nemchinov, "Consequences of Impacts of Cosmic Bodies on the Surface of the Earth," Hazards Due to Comets and Asteroids, ed. Tom Gehrels (Tucson: The University of Arizona Press, 1994), 722.
^ Charles T. Kowal, Asteroids: Their Nature and Utilization, 2nd edition (New York: John Wiley & Sons, 1996), xv.
^ Charles T. Kowal, Asteroids: Their Nature and Utilization, 2nd edition (New York: John Wiley & Sons, 1996), 24.
^ David Morrison, Clark R. Chapman, and Paul Slovic, "The Impact Hazard," Hazards Due to Comets and Asteroids, ed. Tom Gehrels (Tucson: The University of Arizona Press, 1994), 59–91.
^ Clark R. Chapman and David Morrison, "Impacts on the Earth by asteroids and comets: assessing the hazard," Nature 367 (6 January 1994): 33–40.
^ See, for example, Part VII of Hazards Due to Comets and Asteroids, ed. Tom Gehrels (Tucson: The University of Arizona Press, 1994), 897–1132.
^ Gerald E. Aardsma, "The Cause of Noah's Flood," The Biblical Chronologist 3.5 (September/October 1997): 1–14 and Gerald E. Aardsma, "Research in Progress," The Biblical Chronologist 3.6 (November/December 1997): 14–18.
^ Frank D. Stacey, Physics of the Earth (Australia: Brookfield Press, 1992), 454–455.
^ Gerald E. Aardsma, "Research in Progress," The Biblical Chronologist 3.6 (November/December 1997): 16.
^ Gerald E. Aardsma, "The Cause of Noah's Flood," The Biblical Chronologist 3.5 (September/October 1997): 12–13, and Gerald E. Aardsma, "Zoogeography and Noah's Flood," The Biblical Chronologist 4.1 (January/February 1998): 1–7.
^ Clark R. Chapman and David Morrison, "Impacts on the Earth by asteroids and comets: assessing the hazard," Nature 367 (6 January 1994): Table 2, page 36.
^ Gerald E. Aardsma, "Research in Progress," The Biblical Chronologist 4.1 (January/February 1998): 11–16.
^ Gerald E. Aardsma, "The Cause of Noah's Flood," The Biblical Chronologist 3.5 (September/October 1997): 10–12.
^ Vitaly V. Adushkin and Ivan V. Nemchinov, "Consequences of Impacts of Cosmic Bodies on the Surface of the Earth," Hazards Due to Comets and Asteroids, ed. Tom Gehrels (Tucson: The University of Arizona Press, 1994), 726.
^ David Halliday and Robert Resnick, Fundamentals of Physics, (New York: John Wiley & Sons, 1974), 349.
^ John L. Remo, "Classifying and Modeling NEO Material Properties and Interactions," Hazards Due to Comets and Asteroids, ed. Tom Gehrels (Tucson: The University of Arizona Press, 1994), 558.
^ John L. Remo, "Classifying and Modeling NEO Material Properties and Interactions," Hazards Due to Comets and Asteroids, ed. Tom Gehrels (Tucson: The University of Arizona Press, 1994), 590.
^ Joseph W. Kane and Morton M. Sternheim, Physics, (New York: John Wiley & Sons, 1980), 94.
^ Gerald E. Aardsma, "Research in Progress," The Biblical Chronologist 3.6 (November/December 1997): 14–18.
^ Gerald E. Aardsma, "Research in Progress," The Biblical Chronologist 4.1 (January/February 1998): 11–16.
^ Gerald E. Aardsma, "The Cause of Noah's Flood," The Biblical Chronologist 3.5 (September/October 1997): 8.
^ Erik H. Erikson, Childhood and Society, 2nd ed. (New York: W. W. Norton & Company, 1963), 171–172.